Course: Calculus (II)
Instructor: 莊重
Time: 2023 Spring
隨手做的,可能沒有很完整,有看到有趣的題目或是重要的定理或是我想記錄才會放上來。
Sequences
Limit of a Sequence
$$
\lim_{n \to \infty} a_n = L \iff \forall \epsilon > 0, \exists N \ \ s.t. \forall n > N, |a_n-L| < \epsilon
$$
$$
\lim_{n \to \infty} a_n = \infty \iff \forall M > 0, \exists N \ \ s.t. \forall n > N, a_n > M
$$
Discrete v.s. Continuous
$$
\lim_{x \to \infty} f(x) = L, f(n) = a_n \ \forall n \in \mathbb{Z^+} \Longrightarrow \lim_{n \to \infty} a_n = L
$$
Limit + Continuous Function
If $\displaystyle\lim_{n \to \infty} a_n = L$ and $f$ is continuous at $L$, then $\displaystyle\lim_{n \to \infty} f(a_n) = f(\lim_{n \to \infty} a_n) = f(L)$
Monotonic / Bounded
- Increasing: $a_{n} < a_{n+1}$
- Decreasing: $a_{n} > a_{n+1}$
- Monotonic: Either Increasing or Decreasing
- Bounded Above (上面有東西擋住): $\exists M \ s.t. a_n \le M \ \ (\forall n)$
- Bounded Below (下面有東西擋住): $\exists m \ s.t. m \le a_n \ \ (\forall n)$
- Bounded Sequence: bounded above and below at the same time
Monotonic Sequence Theorem
- Increasing and Bounded Above $\Longrightarrow$ convergent
- Decreasing and Bounded Below $\Longrightarrow$ convergent
證明:由 LUB 公理得出存在最小上界 $L$,再利用柯西極限的定義證得。
Monotonic Sequence Theorem 很常出現在後續章節的定理證明,包括 Intergral Test、Comparison Test、Alternating Series Test (Even Partial Sum 收斂的證明)。
Series
Convergence Tests for Series
- $a_n$ 一定要收斂到 0
$\displaystyle \sum_{n=1}^{\infty} a_n$ is convergent $\Longrightarrow$ $\displaystyle \lim_{n \to \infty} a_n = 0$
$\displaystyle \lim_{n \to \infty} a_n \ne 0$ $\Longrightarrow$ $\displaystyle \sum_{n=1}^{\infty} a_n$ is divergent
$\displaystyle \lim_{n \to \infty} a_n = 0$ $\not\Longrightarrow$ $\displaystyle \sum_{n=1}^{\infty} a_n$ is convergent (Counter Example: $\displaystyle \sum_{n=1}^{\infty} \frac{1}{n}$)
.
- 最單純的級數:p 級數、幾何級數
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p (\ln n)^q}$ is convergent if $p > 1$ or $p = 1, q > 1$
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p (\ln n)^q}$ is divergent if $p < 1$ or $p = 1, q \le 1$
幾何級數就看公比:$|r| < 1$
.
- Integral Tests
使用條件:
- $a_n$ 是正項級數(全部都負的話就翻成正的)
- $a_n$ 遞減,可用 $f’(x)$ 的正負來判斷是否遞減。
$\sum_{n=1}^{\infty} a_n$ 的斂散性和 $\int_{1}^{\infty} f(x) dx$ 相同。
證明:
收斂的部分用 DCT + MST 證:
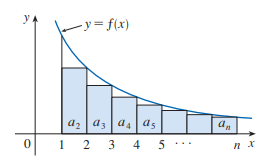
發散的部分用 DCT 證:
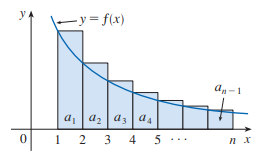

數論裡面一些演算法的時間複雜度、函數成長速度就是用積分估算的。
調和級數:$\displaystyle \sum_{n=1}^{N} \frac{N}{n} \approx \int_{1}^{N} \frac{N}{x} dx = \Theta(N \log N)$
杜教篩:$\displaystyle N^\frac{2}{3} + \sum_{n=1}^{\lfloor N^{1/3} \rfloor} \sqrt{\frac{N}{n}} \approx N^\frac{2}{3} + \int_{1}^{N^{1/3}} \sqrt{\frac{N}{x}} dx = O(N^\frac{2}{3})$
.
- Comparison Tests
使用條件:
- $a_n$ 是正項級數(全部都負的話就翻成正的)
有分成 DCT 跟 LCT,但形式都滿單純的所以就不寫上來。
DCT 證明可以用 MST,而 LCT 證明可以先設 $m < a_n/b_n < M \Rightarrow mb_n < a_n < Mb_n$ ,得出上下界後用 DCT。
.
- Alternating Series Test
使用條件:
- $a_n$ 是交錯級數
以下兩個條件都要驗證,注意不能只驗證第 2 個:
- $|a_n|$ 非嚴格遞減,即 $|a_n| - |a_{n+1}| \ge 0$
- $\displaystyle \lim_{n \to \infty} |a_n| = 0$
其實把 $s_n$ 放到數線上的話,不難發現 $s_n$ 會來回跳動,非嚴格遞減、收斂到 0 這兩個條件可以保證每次跳動的長度越來越小,振幅越小最後就會收斂在某個點上。
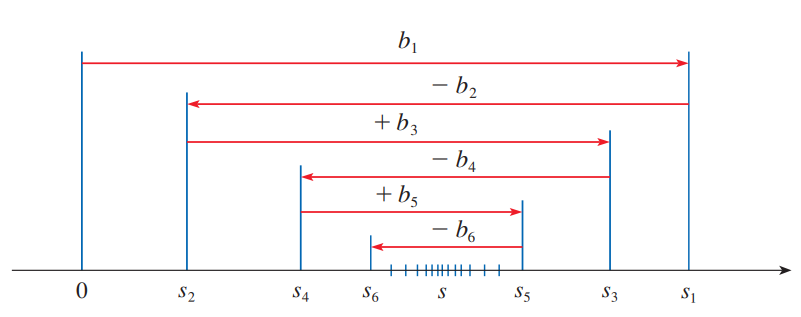
證明的話也很單純,以最後收斂的和 $s$ 作為分界點,會發現其中一邊是奇數另外一邊是偶數。先選擇其中一邊來證明收斂 (by MST),最後另外一邊的證明就只要補上某一項讓奇偶性反轉,就可以不用兩邊都做 MST。
.
- Ratio/Root Test
Ratio Test: Let $\displaystyle r = \lim_{n \to \infty} |\frac{a_{n+1}}{a_n}|$
Root Test: Let $\displaystyle r = \lim_{n \to \infty} \sqrt[n]{|a_n|}$
If $r = 1 \Longrightarrow$ converge.
If $r > 1 \lor r = \infty \Longrightarrow$ diverge.
If $r = 1 \Longrightarrow$ fail.
事實上兩個 Test 等價,即:
$$
\lim_{n \to \infty} |\frac{a_{n+1}}{a_n}| = r \Longleftrightarrow \lim_{n \to \infty} \sqrt[n]{|a_n|} = r \quad \text{(Cauchy’s Second Theorem on Limits)}
$$
餘項估計
定義 $s$ 為 $\displaystyle \sum a_n$ 收斂到的值。
定義 $\displaystyle R_n = s - s_n = \sum_{k = n+1}^{\infty} a_k$。
有時候級數和沒有特定公式可以計算,只能取前面有限個項,餘項估計就是在考慮只取有限個項的情況下產生的誤差。
Integral Test
$\displaystyle \int_{n+1}^{\infty} f(x) dx \le R_n \le \int_{n}^{\infty} f(x) dx$
$\displaystyle s_n + \int_{n+1}^{\infty} f(x) dx \le s \le s_n + \int_{n}^{\infty} f(x) dx$
Alternating Series Test
$|R_n| \le |a_{n+1}|$