比賽資訊
- 題目:https://tioj.ck.tp.edu.tw/contests/81
- 計分板:https://tioj.ck.tp.edu.tw/contests/81/dashboard
- 題解:https://hackmd.io/@Dn7ABYK4QAyS02iuO5ydBw/rJvk_9oBY#/
比賽結果
嚴格來說其實超時了 9 分鐘
雖然對不起良心但我不管(X,反正第一次賽中幹出懶標線段樹就是爽
Subtasks Gained
Tried and Accepted
Tried but in Vain
Supposed to Try / Easy Subtask
pA 10/21/10/16/43
pB 7/10/13/15/20/35
pC 6/7/10/15/11/12/39
pD 36/64
pE 6/9/12/24/21/24/14
Final Score/Rank
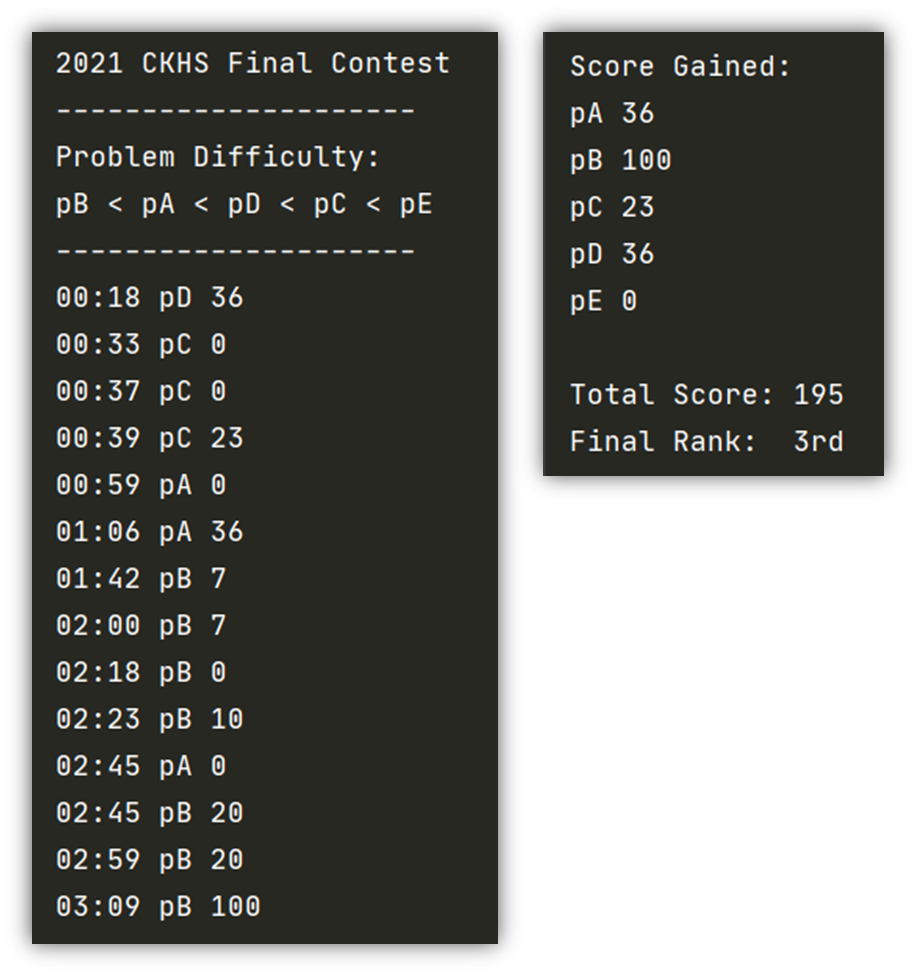
比賽過程
賽前已經被暴雷記分板了,一片慘況甚至連 cheissmart 都沒有破台,大概心理有底這次的題目很難。
於是開賽時我打算先把能撈的分撈一撈,沒想到這策略意外奏效。
花了 12 分鐘讀題目,但這次題敘都不算難懂,所以還是讀得有點慢zzz。對題目的理解大概如下:
pA:$Q$ 次詢問帶邊權樹上 $u, v$ 兩點,求 $u, v$ 兩點的路徑長,但每次詢問完後會把 $u, v$ 路徑上的所有邊權歸 $0$。有想了一下但只想到樹鍊剖分,而且我完全不會刻zzz。
pB:給一個序列,兩種屬性 $m, v$(質量跟速度),維護區間動能和 $(\sum \frac{1}{2} mv^2)$,操作有區間質量/速度加值,就裸的懶標線段樹,但要維護一堆東西而且一不小心就會有 overflow 的生命危險,滿麻煩的實作。
pC:邊權皆 $> 0$ 的圖上,每條邊皆有顏色,在不連續走相同顏色邊的限制下,求全點對最短路徑和。感覺是 FW 的變形但沒想法。
pD:有趣互動題,$36$ 分簽到分,但剩下的 $64$ 分可能可以隨機,但一點頭緒都沒有QQ。
pE:當下讀完題目覺得有點分治(?),但還是完全沒想法。有 $12$ 分是區間DP,$6$ 分很水但沒有好好想,賽後才發現其實根本就簽到分啊QQ。
pD 36 分最水,決定先拿掉,5 分鐘打好模板 + 寫完就丟上去了。
00:18 pD 36
pC 23 分裸 FW,三層迴圈幹下去就拿得到了,但題目沒看清楚又吃了 2 次 WA,有夠智障。
00:33 pC 0
00:37 pC 0
00:39 pC 23
去上個廁所,休息了大概 3 分鐘。
pA 36 分只要 $O(n^2)$ 暴力就可以了,但我不知道為什麼我寫了 17 分鐘,有夠久。
00:59 pA 0
確定不是智障 bug 後,想了一下才發現 bug 跟我的實作方式有關,修一下之後就過了。
01:06 pA 36
pB 7 分前綴和,10 分 $O(NQ)$,pE 18 分也頗水。但我對 pB 滿分滿有信心的,於是決定開始刻 pB,並利用子題當作分段 checker。
休息了 3 分鐘,推了一下式子確定線段樹沒問題後就開始寫。
先刻好 query 的部分,丟上去穩穩拿 7 分。
01:42 pB 7
接下來是區間質量修改,假設增加質量為 $d$,則式子如下:
$$
\sum \frac{1}{2}(m_i + d)v_i^2 = \frac{1}{2} \sum (m_iv_i^2 + d v_i^2) = \frac{1}{2} (\sum m_iv_i^2 + d\sum v_i^2)
$$
所以多維護的 tag 有 $v_i^2, v_i$。
懶標 push 刻完之後丟上去結果 WA。
02:00 pB 7
然後自己生了一些測資 + 檢查 code,但都沒找到 bug。
意識到這樣下去會燒雞,所以切換成撈分模式。先從 $NQ \leq 10^6$ 的 10 分開始撈。
02:18 pB 0
發現加值的時候忘記取模,其實那筆 subtask 是 WA 但我看到一坨 TLE 擠在一起的時候以為模的常數太肥,所以我在加了 mod 之後又修了一下寫法降低模運算的次數。(後來發現我改了寫法速度根本沒差多少,改辛酸的)
02:23 pB 10
跑去撈 pA 的 21 分,我想說只是抄 pB 的 code 過去修改一下,結果又不知道為什麼寫爛掉。又跳回去看 pB 的 code,又生了一些測資來 debug,但都沒有找到問題。
上個廁所回來,發現 modify 函式不太對勁。
1 | modM(ql, qr, d, l, mid, cl); |
右推函式少打一個參數,幹。
怎麼又是這種智障 bug。
02:45 pB 20
結果 pA 還是爛的 QQ。
02:45 pA 0
這時候想說 pB 修改既然都沒問題了,決定放掉 pA 也放掉 pE 的子題,專心拿滿分。
繼續推區間速度修改的式子,假設增加速度為 $d$,則式子如下:
$$
\sum \frac{1}{2}m_i(v_i + d)^2 = \frac{1}{2} \sum m_i(v_i^2 + 2dv_i + d^2) = \frac{1}{2} (\sum m_iv_i^2 + 2d\sum m_iv_i + d^2 \sum m_i)
$$
所以多維護的 tag 有 $m_iv_i, m_i$。
寫完丟上去,沒過。
02:59 pB 20
比賽時間雖然到了,但我不論如何都想寫出來,所以就當作比賽延長繼續打。結果才發現有一條式子多乘了不該乘的東西。有夠智障。
03:09 pB 100
AC 的當下真的好爽,但頭也好暈XD,休息一下後收一收東西就離開圖書館了。
Score: 195/500, Rk: 3
賽後檢討
這要是正式賽我一定會炸得很難看,沒寫 pE 真的是致命傷。
- 智障 bug:線段樹少打一個參數,多乘不該成的數字。
- 寫 code 的速度太慢。
- pE 犯了 0 分的大忌,千萬不要對某題的滿分解太有自信而不撈其他題的分數。
總體來說,先撈分的策略應該還不錯,至少對穩住心態很有幫助,以後就繼續維持這策略吧。